なぜ文系は理系、理系は文系を学ぶべきか

MITのMBAシリーズ１「オペレーション・マネジメント」

MIT(マサチューセッツ工科大学院）ビジネススクール・スローンフェローMBA(経営学修士）の夏学期をオンラインで受け始めて、1カ月半が過ぎました。いったい何をどういう風に学び、そこから何をTake Away（持ち帰っている）のか。「MITのMBAシリーズ」として、きょうは届けたいと思います。

これまでのNewletter記事を読んでくださった出版社のプロ編集者から「出版に向けて、エッセーで終わらないように」とのアドバイスをいただきました。この言葉も胸に、MBA科目で教わる学問を話題にするというよりは、私たちの日常にどのような気づきやヒントがありそうか、というゴールに向かって書きます。

第１回は、必修科目のIntroduction to Operations Management （オペレーション・マネジメント入門）です。まだ受け始めて２週目なので全体像をとらえきれていませんが、理系と文系の思考や発想の違い、さらに折り合いについて考えるよき題材になっています。

　　◇

神戸港をのぞむメリケンパークを歩いた時のことです。BE KOBEというインスタ映えするモニュメントが人気の場所。昼下がり、小さい子ども連れの家族らが、簡易のテントやレジャーシートを広げて、ボールを遊びをしたり、走り回ったりと、休日を楽しんでいました。暑すぎず、涼しすぎず。木陰に座っているだけで心地よさを感じらるテレビコマーシャルの一コマのような時間でした。

帰り道に「ソフトクリーム」というのぼりに誘われて、近くの売店を訪ねました。店内は大繁盛で、注文受付のカウンターに近づくと、「順番にしばらくお待ち下さい」というプレートが置かれました。

店員は男女の二人。ホットドッグのパンをトースターで焼いたり、かき氷を入れたり、ドリンクをカップに注いだりと、大忙しの様子です。調理場の導線が悪く、二人は行ったり来たり、ぶつかりそうになっていました。

入店から注文を聞いてもらえるまで、10分は待ちました。回りのお客さんも、みんな待ちくたびれていました。「もうこれ以上は待てない」といった様子で、店をあとにするお客さんの姿も見かけました。

店側からすれば、もっと稼げたはずなのに逃した「機会損失」です。客の入店→注文→会計→調理→商品受け渡しについて、効率よく回せたら、たくさん「もうけられる」はずです。

ただ、いつどのタイミングで何人の客が来るのか。注文の料理と量によって、使う時間も違う。店員が何人で対応すべきかも、客の入り次第。色々な不確定要素が絡みます。この最適化を考えるのが、MBAでは「オペレーション・マネジメント」です。

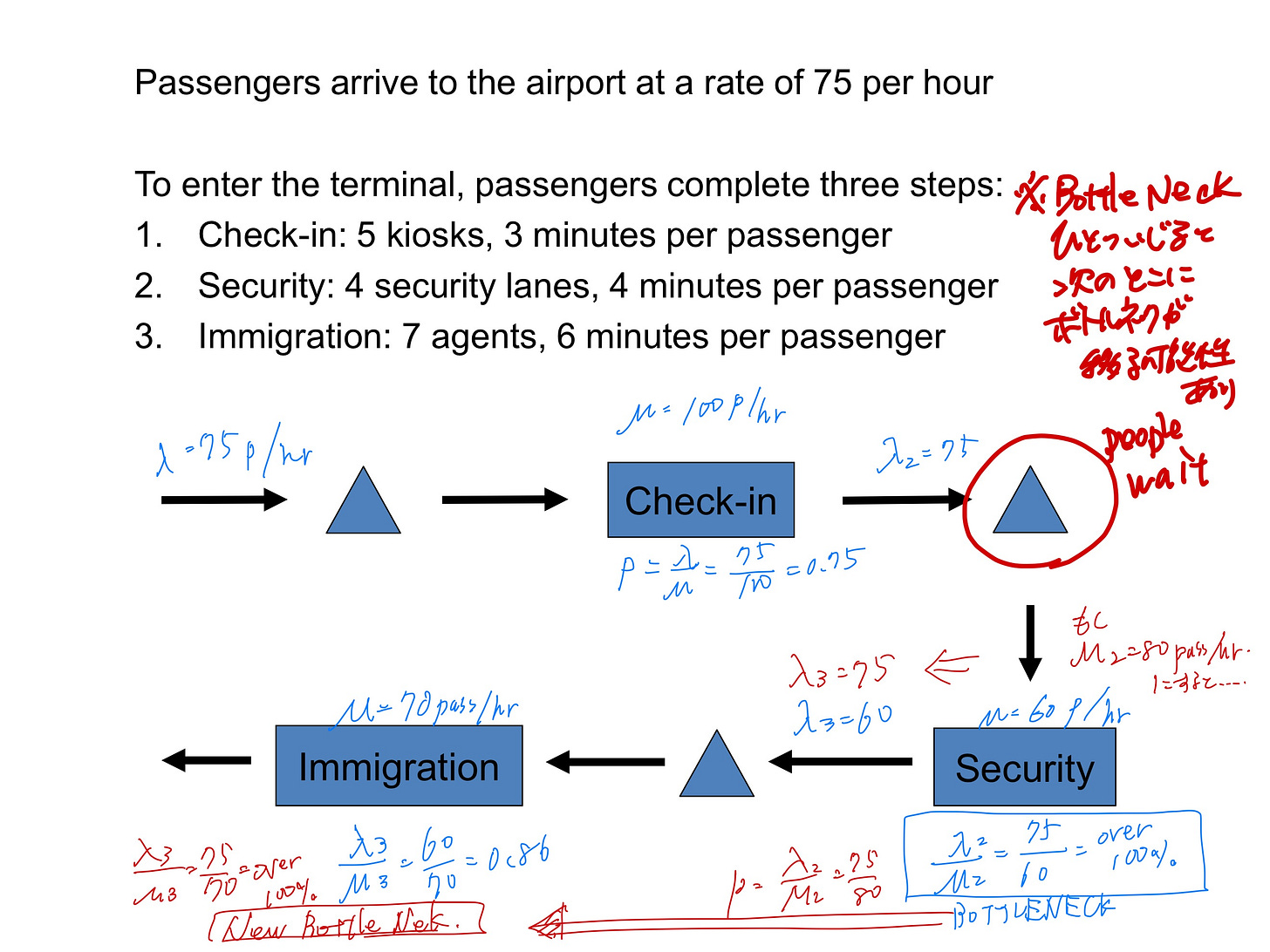
アイスクリーム屋や空港の搭乗手続きを例に学びました。店が1分間に3人にアイスクリームを提供できるとして、平均6人の客が並んでいるとする。平均の待ち時間は？　空港ターミナルで、①チェックイン→②セキュリティーチェック→③イミグレと進む際、どのポイントが人を滞留させる「ボトルネック」になっているか……。

こんな図を描いて考えます。

「うわっ、なんだか難しそう」

「うわっ、なんだか面白そう」

受け止めは、真っ二つにわかれるのではないでしょうか。

文系の大学を出た私は、こういう数字や数式をみると、心理的な抵抗感を抱きがちです。このため、アイスクリーム屋や空港の搭乗手続きといった単純化した例で習い、かろうじて「何をやろうとしているのか」を理解していきます。こころの中では、「できればあまり数式を使わずに今後は進んでほしい」と願うものです。

この講義を受けもつのは、自ら創業した80名程度のオペレーションシステムの会社をNikeに売却したという経歴をもつスタンフォード大卒の教授です。Let me ask you～といって、挙手を促しますが、わたしは答えに自信がないので、なかなか手が重い。

一方、理系の大学院を出た数学が得意なクラスメートのある友人は、講義1日目を終えた段階で、「ものすごく面白い。消費者目線でいえばまったく意識しなくてよいことだけど、世の中の『みえている人たち』は、こういう視点で分析してシステムを作っているのではないか。MITに来て初めて良かったと思えるほど、この講義には期待している」と、興奮ぎみに話しました。

日本語で関連する教科書を探して流し読みしました。「オペレーション戦略」の本はあっても、ほとんど数字を使っていない印象です。アメリカならではなのか、MITならではなのか、現時点ではわかりませんが、とにかく私が受けている講義は数字のオンパレードです。今日の講義でも、λ（ラムダ）やν（ミュー）、Decision Valuable（決定係数）、STD（標準偏差）といった用語が頻繁に飛び交っていました。

文系の私と理系の彼の二人で、チーム課題で出されたケース「マサチューセッツ（MA)州の病院のオペレーション改善」についても話しました。

この病院はMA州トップの医療レベルで患者の支持も厚いのだけれども、とにかく待ち時間が長い。患者からクレームに近い改善要望の手紙が届いた、という設定です。

患者ごとに集めた来院から待機、受診、退院までにかかった時間のデータと、病院側の態勢を元に、滞留を引き起こしている「ボトルネック」を割り出す。そして、どこをどう変えれば、待ち時間の改善がどれぐらい望めるか。そんなことを定量的に考えます。

友人はエクセルで緻密に平均の待ち時間を計算して、人余りの場所で人員削減をして、人が足らないところに回す、という提案を考えていました。

フォントの小さい数字やグラフが画面にびっしり並んだ分析結果を共有しながら、彼がこんな話をしました。

「これ実際のところは、病院内を歩いたら、どこで患者がたまって大忙しで、どこのスタッフがスマホゲームばっかやって暇つぶしをしているか、すぐわかるはず」

確かに数式やグラフ、データをこねくりまわさなくても、わかりきった話です。

私が神戸でソフトクリームを注文した店でも、「非効率さ」がどこにありそうか、というのは誰の目にもハッキリしていました。週末のどの時間帯に客が多めに来るといったことも、わかっていることでしょう。例題でみた、アイスクリーム屋もしかり、空港の搭乗手続きでも、同様のことが言えます。

ではなぜ、一見わかりきった話に、わざわざ定量的アプローチをかけるのか。

ジャカルタの小さな事務所で現地スタッフを預かった私なりに考えて、話しました。

「確かに院内を回ったら、スマホゲームばっかやってるスタッフをすぐ見つけられそうですね。ただ、そこで辞めてもらう、もしくは配置転換させたいときに、何となく『君たち、暇そうだから、辞めてもらえるかな』と言っても反発を受けそうです。場合によっては、急に忙しそうに振る舞われるかもしれません。その検討会議で、『あそこは大事なポジションだ』と反対されることもあるでしょう。そういう時に数字の出番じゃないでしょうか」

データの分析結果を根拠として示しながら、説得していく。そのための定量分析だと思いました。理系思考・ハードスキルの出番です。

一方、こうした数字の根拠があれば、万事うまくことが進むか？といえば、そういう単純な話でもないでしょう。退職や配置転換といった説得には、リーダーシップや交渉力、また定性的な分析も欠かせません。どちらかといえば文系思考・ソフトスキルを働かせるときです。

私が長らく働いてきた新聞社は文系の仲間が多く、理系のMITで数字が得意な同級生と出会い、こうした会話ができるのは、とても新鮮で楽しいです。

「答えが出ない問題は気持ちが悪い」と話す彼が、文系的なアプローチも磨いてく。

「答えがハッキリしている問題をよく間違える」と嘆く私が、理系的思考を伸ばす。

オペレーション・マネジメントは、そんなきっかけとなりそうなMBA科目です。